NOIP2014 普及组
T1:珠心算测验
题目描述
珠心算是一种通过在脑中模拟算盘变化来完成快速运算的一种计算技术。珠心算训练,既能够开发智力,又能够为日常生活带来很多便利,因而在很多学校得到普及。
某学校的珠心算老师采用一种快速考察珠心算加法能力的测验方法。他随机生成一个正整数集合,集合中的数各不相同,然后要求学生回答:其中有多少个数,恰好等于集合中另外两个(不同的)数之和?
最近老师出了一些测验题,请你帮忙求出答案。
输入格式
共两行,第一行包含一个整数,表示测试题中给出的正整数个数。
第二行有个正整数,每两个正整数之间用一个空格隔开,表示测试题中给出的正整数。
输出格式
一个整数,表示测验题答案。
输入输出样例
输入样例 #1
4
1 2 3 4
输出样例 #1
2
说明/提示
【样例说明】
由,故满足测试要求的答案为。
注意,加数和被加数必须是集合中的两个不同的数。
【数据说明】
对于的数据,,测验题给出的正整数大小不超过
NOIP2014普及组第一题
题解:
本题可以用三重 for() 循环来解决。
与 枚举两个加数, 枚举和。为了避免 重复,我们设置一个数组 来存储 , 表示 已经被使用过, 表示 未被使用过。若满足:
- 、 、 互不相等
- ( 未被使用过)
这三个条件的话,我们便找到了一个答案。最后,输出答案总数就可以了。
#include <iostream>
using namespace std;
int num[101], t[10001];
int main() {
int n;
cin >> n;
for (int i = 1; i <= n; i++)
cin >> num[i];
int ans = 0;
for (int i = 1; i <= n; i++) {
for (int j = i + 1; j <= n; j++) {
for (int k = 1; k <= n; k++) {
if (num[i] + num[j] == num[k] && i != k && j != k && t[num[k]] == 0) {
t[num[k]] = 1;
ans++;
}
}
}
}
cout << ans << endl;
return 0;
}
T2:比例简化
题目描述
社交媒体上,经常会看到针对某一个观点同意与否的民意调查以及结果。例如,对某一观点表示支持的有 人,反对的有 人,那么赞同与反对的比例可以简单的记为。
不过,如果把调查结果就以这种方式呈现出来,大多数人肯定不会满意。因为这个比例的数值太大,难以一眼看出它们的关系。对于上面这个例子,如果把比例记为,虽然与真实结果有一定的误差,但依然能够较为准确地反映调查结果,同时也显得比较直观。
现给出支持人数A,反对人数,以及一个上限,请你将比化简为’比’,要求在’和’均不大于且’和’互质(两个整数的最大公约数是)的前提下,’’且’’的值尽可能小。
输入格式
共一行,包含三个整数,每两个整数之间用一个空格隔开,分别表示支持人数、反对人数以及上限。
输出格式
共一行,包含两个整数’,’,中间用一个空格隔开,表示化简后的比例。
输入输出样例
输入样例 #1
1498 902 10
输出样例 #1
5 3
说明/提示
对于的数据,。
NOIP2014普及组第二题
题解:
考虑到 最多只有 ,因此我们便可以枚举’ 与 ’。
我们用 枚举 ’, 用 枚举 ’。
然后,我们设置变量 存储 ’ , 用 存储 ’ 。那么,我们在枚举’ 与 ’ 时,如何保证 与 得到更新呢?
根据题目要求,’’的值尽可能小。因此,我们便可以得到在 时,更新 与 。
但是, 可以化简。
也就是:
所以,当 , 满足 gcd(i, j) == 1 && b * i >= a * j && j * ansa > i * ansb 时,更新 与 ,最后输出 与 就好啦!
#include <iostream>
using namespace std;
int gcd(int x, int y) {
return y == 0 ? x : gcd(y, x % y);
}
int main() {
int a, b, l;
cin >> a >> b >> l;
int ansa = 0x3f3f3f, ansb = 1;
for (int i = 1; i <= l; i++) {
for (int j = 1; j <= l; j++) {
if (gcd(i, j) == 1 && b * i >= a * j && j * ansa > i * ansb) {
ansa = i;
ansb = j;
}
}
}
cout << ansa << " " << ansb << endl;
return 0;
}
T3:螺旋矩阵
题目描述
一个行列的螺旋矩阵可由如下方法生成:
从矩阵的左上角(第行第列)出发,初始时向右移动;如果前方是未曾经过的格子,则继续前进,否则右转;重复上述操作直至经过矩阵中所有格子。根据经过顺序,在格子中依次填入,便构成了一个螺旋矩阵。
下图是一个 时的螺旋矩阵。
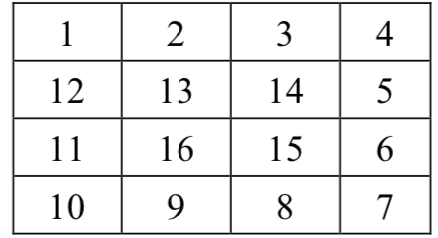
现给出矩阵大小以及和,请你求出该矩阵中第行第列的数是多少。
输入格式
共一行,包含三个整数 ,每两个整数之间用一个空格隔开,分别表示矩阵大小、待求的数所在的行号和列号。。
输出格式
一个整数,表示相应矩阵中第行第列的数。
输入输出样例
输入样例 #1
4 2 3
输出样例 #1
14
说明/提示
【数据说明】
对于的数据,;
对于的数据,。
题解:
很明显,这个提示一个找规律的题呗!
我们可以将大矩阵分成一层一层的小矩阵:
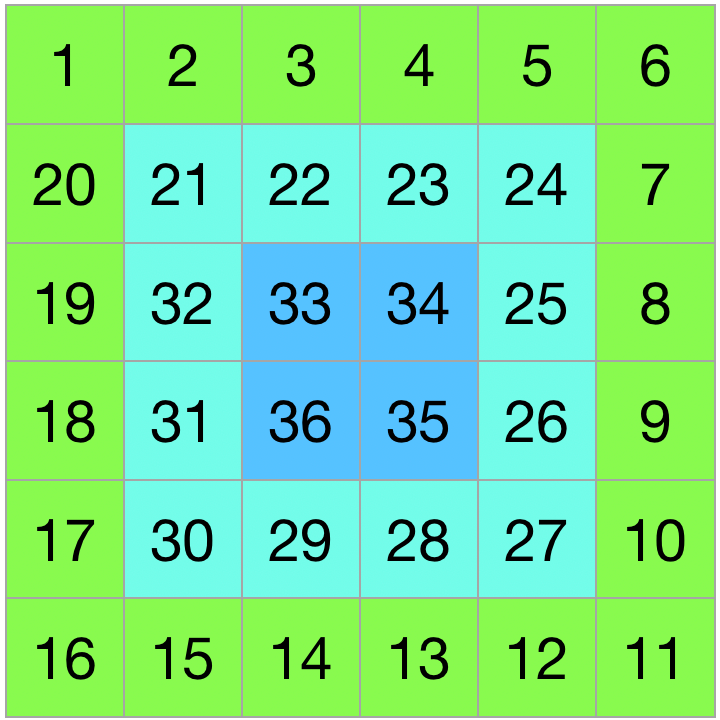
然后,我们先研究如何在一个小矩阵里面找到一个坐标:
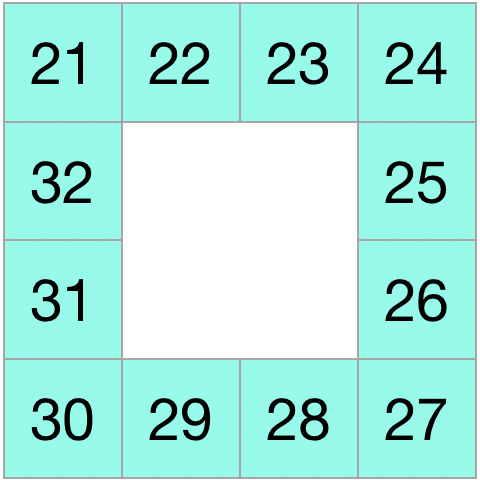
假设我们知道这个小矩阵左上角的数字是多少,如果我们要找在这个小矩阵寻找一个数字,应该怎样找呢?
- 当 时,也就是在第 行寻找一个数字。我们直接返回左上角的数字 就可以。
- 当 时,也就是在第 行寻找一个数字。这个小矩阵的大小 是 ,因此,我们先将 得到左下角的坐标,然后再 得到我们要找的坐标,最后,将这个坐标 左上角的数字就是我们要找的数字了!
- 当 时,也就是在第 列寻找一个数字。同情况 一样,我们先将将 得到左上角正下方数字 的坐标,然后再 得到我们要找的坐标,最后,将这个坐标 左上角的数字就是我们要找的数字了!
- 当 时,也就是在第 列寻找一个数字。我们直接返回左上角的数字 就可以。
然后,我们可以通过递归来得到小矩阵。并且在递归过程中,我们可以不断将当前 得到当前矩阵左上角的数字。最后输出答案就好辣!
#include <iostream>
using namespace std;
int find(int n, int i, int j) {
if (i == 1)
return j;
if (i == n)
return (n - 1) * 3 - j + 2;
if (j == 1)
return (n - 1) * 4 - i + 2;
if (j == n)
return n + i - 1;
return find(n - 2, i - 1, j - 1) + (n - 1) * 4;
}
int main() {
int n, i, j;
cin >> n >> i >> j;
cout << find(n, i ,j) << endl;
return 0;
}
T4:子矩阵
题目描述
给出如下定义:
-
子矩阵:从一个矩阵当中选取某些行和某些列交叉位置所组成的新矩阵(保持行与列的相对顺序)被称为原矩阵的一个子矩阵。
例如,下面左图中选取第、行和第、、列交叉位置的元素得到一个的子矩阵如右图所示。
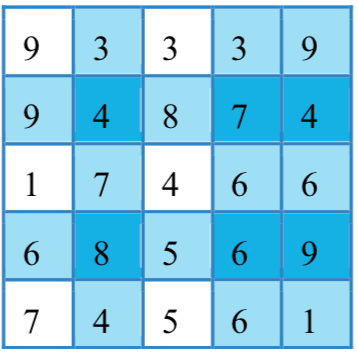
的其中一个的子矩阵是
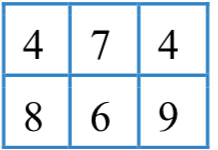
-
相邻的元素:矩阵中的某个元素与其上下左右四个元素(如果存在的话)是相邻的。
-
矩阵的分值:矩阵中每一对相邻元素之差的绝对值之和。
本题任务:给定一个行列的正整数矩阵,请你从这个矩阵中选出一个行列的子矩阵,使得这个子矩阵的分值最小,并输出这个分值。
输入格式
第一行包含用空格隔开的四个整数,意义如问题描述中所述,每两个整数之间用一个空格隔开。
接下来的行,每行包含个用空格隔开的整数,用来表示问题描述中那个行列的矩阵
输出格式
一个整数,表示满足题目描述的子矩阵的最小分值。
输入输出样例
输入样例 #1
5 5 2 3
9 3 3 3 9
9 4 8 7 4
1 7 4 6 6
6 8 5 6 9
7 4 5 6 1
输出样例 #1
6
输入样例 #2
7 7 3 3
7 7 7 6 2 10 5
5 8 8 2 1 6 2
2 9 5 5 6 1 7
7 9 3 6 1 7 8
1 9 1 4 7 8 8
10 5 9 1 1 8 10
1 3 1 5 4 8 6
输出样例 #2
16
说明/提示
【输入输出样例1说明】
该矩阵中分值最小的行列的子矩阵由原矩阵的第行、第行与第列、第列、第列交叉位置的元素组成,为
6 5 6 7 5 6
,其分值为:
【输入输出样例2说明】
该矩阵中分值最小的3行3列的子矩阵由原矩阵的第行、第行、第行与第列、第列、第列交叉位置的元素组成,选取的分值最小的子矩阵为
9 7 8 9 8 8 5 8 10
【数据说明】
对于的数据,,矩阵中的每个元素;
对于的数据,,矩阵中的每个元素。
题解:
本题采用 的方式,先枚举行的排列情况,再 出列的最优情况。代码注释也比较多,这里就不详细写了。
#include <cmath>
#include <cstring>
#include <iostream>
using namespace std;
int n, m, r, c; //在 n 行 m 列的矩阵中选出一个 r 行 c 列的子矩阵
int matrix[21][21]; //存储大矩阵
int column[21]; //column[i] 指第 i 列所有元素的值
int between[21][21]; //between[i][j] 指的是第 i 列与 j 列中,所有同行的元素差的绝对值之和
int choose[21], choosei = 1; //已经选择的列
int ans = 0x3f3f3f; //存储答案
int f[21][21]; //f[i][j] 表示在 r * m 的矩阵中,在前 i 列中选择 j 列
void initialize () { //初始化
memset(column, 0, sizeof(column)); //清空 column
for (int i = 1; i <= m; i++) //处理 line[i]
for (int j = 1; j < r; j++)
column[i] += abs(matrix[choose[j + 1]][i] - matrix[choose[j]][i]); //第 i 列元素的值
//初始化 column 完毕!
memset(between, 0, sizeof(between)); //清空 between
for (int i = 2; i <= m; i++) //处理 between
for (int j = 1; j < i; j++) //为什么 j 要从 1 -> i 呐?因为 between[i][j] 的作用指的是between[i][j] 指的是第 i 列与 j 列中,所有同行的元素差的绝对值之和。所以。。。如果 j > i 的话,没有任何意义滴!
for (int k = 1; k <= r; k++) //枚举行
between[i][j] += abs(matrix[choose[k]][i] - matrix[choose[k]][j]);
}
void DP () {
for (int i = 1; i <= m; i++) { //枚举列
for (int j = 1; j <= min(i, c); j++) { //在前 i 列中选择 j 列,求 f[i][j]
f[i][j] = 0x3f3f3f; //取 INF
if (j == 1) //边界条件 1 :只选择一列的话,那么最小值也就是我们求出的 column[i]
f[i][j] = column[i];
else if (i == j) //边界条件 2 :i 列全选,则最小值就是 i - 1 列全选的最小值 + 选择这一列的最小值 + 第 i 列与第 j - 1 列同行的元素差的绝对值之和
f[i][j] = f[i - 1][j - 1] + column[i] + between[i][j - 1];
else
for (int k = j - 1; k <= i - 1; k++) //若 k < j - 1 的话,那么f[k][j - 1]便不存在了
f[i][j] = min(f[i][j], f[k][j - 1] + column[i] + between[i][k]);
if (j == c) //选取完了 c 列
ans = min(ans, f[i][j]); //更新答案
}
}
}
void DFS (int node);
void PUT (int node) {
choose[choosei] = node;
choosei++;
DFS(node + 1); //继续枚举
choose[choosei] = 0; //还原现场
choosei--;
}
void DFS (int node) { //枚举行的排列情况,以 DP 出列的最优情况
if (node > n) { //已经枚举完毕行,跑一遍初始化与 DP
initialize();
DP();
return;
} else if (n - node == r - choosei) { //剩下的需要全选
PUT(node);
return;
}
//👇下面分两种情况:不选取 node ,选取 node
DFS(node + 1); //不选取 node
//选取 node
if (choosei <= r) //还没选够 r 行呢!可以继续选取!
PUT(node);
}
int main() {
cin >> n >> m >> r >> c;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
cin >> matrix[i][j];
DFS(1);
cout << ans << endl;
return 0;
}
